Improper Fractions are easy to understand, if you have some one who can explain it in a way that you can understand.
"No concept is beyond the child if it is explained at the child's level."
This lesson can go a lot of ways, it can be a fractions lesson, it can be combined with a measurement lesson, it can be in introduction to more fractions concepts, it can be an introduction to algebra concepts, it can be a lesson on division and multiplication....in the video I was accompanied by a peanut gallery consisting of a 4 and 5 year old and the lesson was for an Autistic child so I kept it simple and we did fractions, measurement and multiplication and division....but above all all we did was COUNT and that's the way we always start.
The fraction has the what kind part and the how many part all in one place, the top tells how numerous the numerator and the bottom tells d'nom, the nom, the name of it: the denominator. When the denominator is bigger than the numerator we call this an improper fraction because there are whole numbers hiding in there...our job is to find out how many. Let's start with 7/2 = ?
It's easy for the student to count how many twos are contained in 7 or to measure 7 with 2's. They can see that we are counting 2's and there are four of them of them...but wait we only can count THREE whole ones and we use a part of the fourth one, one out of two parts and we call that one half...
In this problem we ended up using 3 of 6 and so we did a couple of lesson on reducing fractions. There are several ways to explain it.
We can look at the relationship, it's one to two, one three on top two three's on the bottom.
We can expose the common factor of three by turning them on their sides, and counting the edges 1 x 3 / 2 x 3 and see 3/3 is ONE.
We can still see the ratio of one to two if we look. You need to do many problems like this for them to be able to do these easily but start off small so they get the CONCEPTS under their belt first.
Here is a short vid explaining these concepts with comments and button pushing by the four year old:
Find us on FaceBook
Go to the House of Math.


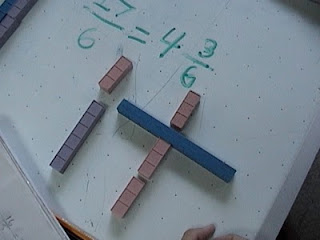


No comments:
Post a Comment