In the first part of the video you see him factor a problem he's never seen before:
x2 + 8x + 12
The day and week before, he has already done x2 + 8x + 16 a couple of ways once as a problem for completing the square:
x2 + 8x + ?? ?? = What completes the square?
and once as a problem for factoring where he got all the info:
x2 + 8x + 16 and we talked about (x+4)2.
To make it a bit of a challenge I changed it to x2 + 8x + 12. But he's almost at the point where they are all EASY.
Note how his brother builds squares and the quietly arranges them according to size while I am focused on his brother...he received a lot of praise off camera when we reviewed this video together.
Then we played with the concept of squaring the sides of a triangle.
If you build the lesson correctly where your students have to play with the triangles and tell YOU about the relationships (instead of the other way around) you will find 90% of your students will come back with
a2 + b2 = C2!!!
We can also see that later when they see
a2 = c2 - b2 or
b2 = c2 - a2
it will make total sense to them.
This was just the first time they saw this and they will see it many times again before they reach the ripe old age of 7...note how in the video I didn't even write out the equation. We just played with the blocks and got an experience of the concepts. Next time when we do write the symbols that go along with the blocks they will understand what it means instead of just memorizing a formula.
They will also see that a + b > c ALWAYS, although they may make the joke 3 + 4 = 5 they will know it's a joke and that 32 + 42 = 52 is true but 3 + 4 = 5 isn't.
Also note how much faster and easier this lesson is now that they each can skip count by 3's 4's and 5's...and this lesson gave then another chance to practice skip counting.
Stay tuned for an additional video that is a more formal lesson for YOU on Pythagorean Theorem sans little children where we can see how to make "Pythagorean Triples" and understand more about the theorem before we ever have to get out our square rooting skills for numbers that aren't perfect squares.
I talked to a few teachers who never saw a proof of this...they just got the formula and memorized it. I talk to teachers all the time that are amazed by this little demonstration...INCLUDE it in your lessons with little kids.
The House of Math on FaceBook.
The House of Math
Learn algebra for a buck.
Pythagorean Theorem at the House of Math.
“It isn't enough just to learn -- one must learn how to learn, how to learn without classrooms, without teachers, without textbooks. Learn, in short, how to think and analyze and decide and discover and create." -- Michael Bassis
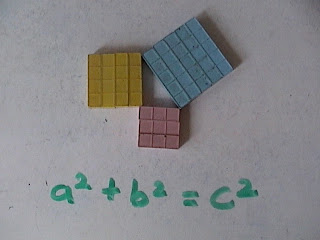
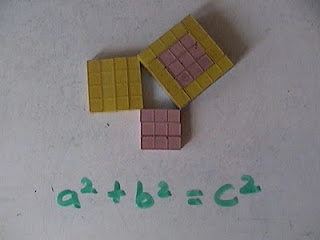
No comments:
Post a Comment