Using Algebra To Teach Basic Operations.

The basic operations are usually defined as addition, subtraction, multiplication and division. Algebra, because it is generic math can get the basic concepts across quickly and easily. Notice that I used the term "generic," much less intimidating than "abstract mathematics".

There are many kinds of base ten blocks that you can purchase, but base ten blocks are not all the same and some are much more useful than others. First off, make sure they are base ten blocks, I have seen block sets where they are base seven and even base three...where seven of the x are same as an x² or just three y are the same as the y² while still quite workable doing the larger problems becomes somewhat difficult because it takes too long to count out the units. This is very much akin to getting lost in computation...many students lose track of the problem they are doing because even if they understand the concepts they can't do the math or it takes them a long time to do the math and they forget what they were doing in the first place.

Here we see a seven year old student doing simple sums with the blocks handy in case he gets stuck...he didn't get stuck. Note there are a few problems where he has to figure out what x is, and to do so he will have to do some subtraction even though all these problems seem to be "addition."
For 7 + x = 15,

He doesn't try to figure out the answer by counting forward he knows two ways to solve it. One he "subtracts" 7 from 15 by using addends...seven needs 3 to be ten (taking the seven out of the ten) and 3 + 5 = 8 or "using up" the five, he can take 5 out of 7 which leaves 2, and 2 needs 8 to be ten...so the answer is 8 either way.

Next we build some simple rectangles in algebra. For the the first problem he got out 3x and a nine (the nine block) but that didn't make a rectangle. He looked at me for help and I just smiled. "Make me a rectangle..."

He puzzles over it for a moment and then you can see the light bulb go on. "I need three 3's!" Now counting the sides is EASY 3 across and x + 3 up...the next one looks "hard" so he skips it and does the last one. I think this is because we spent some time playing with nines and he hasn't had much experience with sevens.

You don't see it here but he got out 9x and then got out nine fours and was able to see that the rectangle was 9x + 36 and the sides were 9 across and x + 4 up.

9x + 36 = 9(x + 4)

Then I showed him that he could have used 4 nines and we talked a little about 9 being the "common factor", but mostly this lesson was about division for him...making 36 "fit" on the 9x...if the whole thing is 36 and one side is 9 what does the other side have to be? Four. Which is why he got out fours...



He did the same thing with 7x + 21 (the problem in the middle, solution pictured and built but the answer isn't written yet)...took him several tries before he got out three's...I asked him why he didn't just get out sevens...he thought for a moment and then went, "OH, now I get it...!"


Next he got to build his own problem and we see that "bigger is funner." I had two top trays out, which meant he had 3x² and 20x to work with so he used all of them. BIGGER IS FUNNER. He spent some time building it and making it so he could use up all the x. Then he fit in the eights and I told him to count it.

"What do you mean?" he said coyly.

"Tell me the whole thing and the sides....he did and then I told him to write it down.



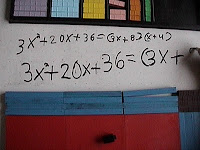
Remember the child is seven, his writing skills are not well developed, first he wrote it too small then he wrote it too big for purposes of the picture but I think he did just fine...it was taking him quite a while to write it and I wanted to move on to the next problem...

The mind wants to work very rapidly, counting out individual units from the various manipulative sets takes too long. Sometimes even counting out tens or x's takes too long. So while sets that have base ten blocks with tens and individual units are quite useful they become tedious if you want to use them to demonstrate many problems in a row or even just a few larger problems. By larger I simply mean problems that will have a lot of pieces to get out. Showing 60% of 80 for example or even a simple problem like (x+6)(x+7) will require getting out 42 units...you already have to get out 13x, counting out 42 units takes a lot of time, and the student can often get lost (and bored) because of it; however, if all you have to do is get out an x-square, 6 sevens (or 7 sixes) and you can grab 7x and 6x, the problem can be built very rapidly.

In this case he had the rectangle

2x² + 20x + 42

And he had to find the sides. Later, when he knows his multiplication better, he will see that the factors of 42 will be a big help in solving this problem quickly, but for now he takes the 20x and makes a rectangle out of that...it took some trial and error to get 6x on top and 14x (two sets of 7x) so that they would fit...that was a lot of counting and adding. Then he still wasn't sure he had it right because he could not tell if 6 times 7 was 42 because he didn't know it. You can see him doing computation on the side...he has 14 three times and the sevens drawn out...again lots of math going on here to figure out if he has 42 or not. 30 + 4 times 3 or 30 plus 12, and then the long way where he has to add seven plus seven plus seven etc until he gets to 42. If he had to count out individual units this problem would have taken MUCH longer and he may not have finished it at all.

2x² + 20x + 42 = (x + 7)(2x + 6)

(In the picture the 2x is cut off.) With a few simple pictures, you can actually SEE what it is I'm talking about. You can see that it becomes easy to teach counting and addition, and multiplication and division using algebra because the child has to count out and add up the blocks in order to build the rectangles needed to solve the problems. At this point you begin to see why a picture is worth a thousand words, and if a picture is worth a thousand words having your hands on the blocks and then being able to draw them is worth a thousand explanations. Further, this is the way the subconscious mind works, using pictures NOT symbols and we have come to realize over the last 100 years that most learning takes place in the subconscious mind not in the conscious mind.

Students who benefit from base ten blocks most are the kinesthetic learners, because they literally can get their hands on algebra and work with the problems. They can see and touch the problems in a very real sense. They can see that x times x is an x square, they can touch it...they see and touch the distributive theory of multiplication because they can see an x+3 is just a number with two parts (a binomial) and if I have 3(x+3) (spoken three times x plus three), I get 3x+9 and they can see it.

Getting this problem out is still easy even if the blocks you have are all individual units, but it's still easier to get out 3 threes...and by the way we can note than 9 is a square number when we build it this way. As soon as you do a problem like 5(x+8) counting out the 40 units is going to slow things down and actually take away from the lesson and the concept that the 5 multiplies the x and the 8. Manipulative sets that use rods to represent numbers are again quite useful but will have serious drawbacks when attempting to demonstrate algebra or square numbers and square roots because most often 3, 3-rods do not make a square. Simple concepts like x + x = 2x are easy for any student who is just learning to count. Base ten manipulatives or base ten blocks can be used for so much more than just counting or to teach addition. When used properly very young students can lean to count and add WHILE they learn algebra and vis-versa, and counting, adding and subtracting lead to multiplication and division.


"We used to think that if we knew one, we knew two, because one and one are two. We are finding that we must learn a great deal more about 'and'." ~Arthur Stanley Eddington, as quoted in A Dictionary of Scientific Quotations" (1991) by Alan L. Mackay, p. 79


Lastly for fun he got to build whatever he wanted. Lots of multiplication went on here as I made him count by nines and fives and tens.


The tens are two fives so we counted pretty high by fives, and we counted all those nines (the teal colored one that make up the roof). Using the "trick" "one less and what does it need?" 6 nines is 54, which means 5 is one less than six and six needs four to be ten...for 14 nines it's two less and what does it need? 14 minus 2 is 12 and 4 needs 6 to be ten so (14)(9) = 126 We also counted by adding nines...

BTW you can check me out on FACE BOOK now...and get up dates etc...and of course get more at Crewton Ramone's House of Math